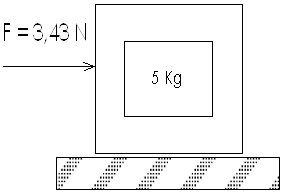
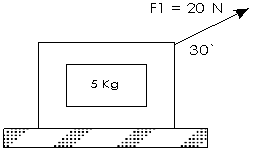
La fuerza de Fricción
El vídeo anterior debe ser visto en su totalidad para que se le consigne progreso en el curso
Algo más, es necesario conocer, que siempre que están en contacto dos cuerpos, hay fuerza de rozamiento entre ellos. Si se mueve un primer cuerpo sobre otro, aparece una fuerza en sentido contrario que se opone al movimiento del primer cuerpo, y es aplicada por el segundo cuerpo en contacto con el primero; ésta se denomina fuerza de fricción o de rozamiento.
Note el detalle aumentado en este ejemplo, de una caja que se mueve sobre el piso:
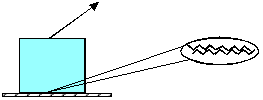
Detalle aumentado de las superficies en contacto, aunque son lisas, a nivel micro son muy rugosas y éste es el origen de la fuerza de rozamiento o fricción.
Si el cuerpo está en reposo, con respecto a un segundo cuerpo (pudiendo el segundo cuerpo ser la superficie), esta fuerza se denomina fuerza de rozamiento estático o de fricción estática, si está en movimiento se denomina fuerza de rozamiento (fricción) cinético.
Esta fuerza siempre se opone al movimiento o sea si un cuerpo se mueve a expensa de una fuerza de 20 N y el rozamiento es 15 N, realmente el cuerpo se mueve solo con una fuerza de 5N. La fricción se representa con f (ojo una f minúscula, pues la mayúscula representa fuerza en general), y se calcula:
| f= μ . N | f= Fuerza de fricción (se mide en N)
μ = Coeficiente de rozamiento, existen dos, si está en reposo se denomina coeficiente de rozamiento estático (μe) y si está en movimiento se denomina coeficiente de rozamiento cinético (μk ). No tiene unidades. N = Normal. Fuerza de contacto aplicada por la superficie del segundo cuerpo en la superficie del primer cuerpo. Es la fuerza de reacción, en este tema corresponde a la fuerza con que el piso sostiene.
|
Aunque esta fórmula anterior simplemente se le sustituyen las variables de acuerdo con lo que deseemos calcular para el caso de fuerza de rozamiento cinético:
fk = μk . N
Un detalle importante es que en términos generales para el caso de un cuerpo que se desliza sobre un plano inclinado, el mk se puede conocer a partir del momento exacto en que el cuerpo empieza a moverse mediante la relación mk = tan q donde q es el ángulo crítico de inclinación del plano en el exacto momento donde empezó a moverse.
Y en el caso de la fuerza de rozamiento estático, se debe escribir:
fe ≤ μe . N
Nótese que no hay un = sino un ≤ (menor o igual que), esto se debe a que la fuerza de rozamiento estático aumenta progresivamente a medida que el primer cuerpo incrementa su fuerza sobre el segundo (si eso sucede), por ejemplo:
Si una fuerza de 1 Newton empuja una mesa sobre el piso en forma horizontal, si la mesa no se mueve es porque en las patas de la mesa aparece una fuerza de rozamiento estático equivalente a 1 Newton en sentido contrario, si la fuerza aumenta a 2N y aún no se mueve es porque la fricción estática ha aumentado ahora a 2N en sentido contrario y así continúa hasta que la fuerza de rozamiento estático llega a su umbral (punto máximo) y entonces desaparece la fuerza de rozamiento estático, llamándose ahora fuerza de rozamiento cinético, debido a que ahora se mueve y generalmente es menor que la fuerza que rompió el rozamiento estático.
Dando click Aquí puede ver la demostración.
El cálculo de la Normal
Es importante profundizar algo más en la fuerza normal y su cálculo. Debido a que la fuerza normal es la fuerza con que el piso sostiene al cuerpo sobre él, es una fuerza de reacción (tercera ley de Newton) que tiene el mismo valor que la fuerza con que el cuerpo empuja el piso, por ejemplo:
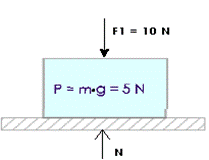 |
En este caso debido a que la caja está sobre el piso y no se está moviendo (hacia arriba o hacia abajo), sino que todas las fuerzas han quedado en equilibrio:
Paso 1. Escribo: ∑Fy= 0 Nota el símbolo ∑Fy solo significa sumar todos los valores en el eje Y. Paso 2. Descompongo ∑Fy: N + – F1y + – P = 0 Paso 3. Despejo N : N = F1y+ P Paso 4. Averiguo el valor de N: N = F1y + Peso = 10N + 5N = 15 N.
|
En este siguiente ejemplo el valor de la fuerza es positivo porque va hacia arriba mientras que el peso es negativo por ir hacia abajo:
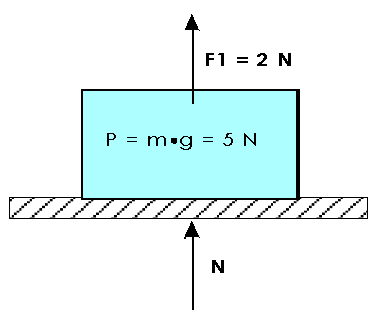
|
Igualmente, la caja está en equilibrio estático, no se está moviendo ni hacia arriba ni hacia abajo, entonces:
∑Fy= 0 N + F1y + -P = 0 N= -F1y + P Nota: F1 es positiva, pasa a negativa. P pasa positiva. N = – F1y + Peso = – 2 N + 5N = 3 N
|
Y ¿qué pasaría si la fuerza para arriba es igual al peso?
Respuesta: El valor de la normal sería cero, la caja estaría sobre el piso, pero no haría ninguna fuerza sobre él, de modo que estaría suspendida.
Ejemplo 3) ¿Cuál es la fuerza de fricción que experimenta la caja, si entre el piso y la caja hay un coeficiente de rozamiento estático de 0,07?, use el siguiente dibujo.
Ejemplo 4) Cual es la aceleración que experimenta la caja, si entre el piso y la caja hay un coeficiente de fricción de 0,07, use el siguiente dibujo. Represente la flecha de la fricción.
Antes de continuar y para reforzar conceptos juega con este laboratorio virtual que te permite profundizar el concepto de fuerza normal y te introduce en el concepto de diagrama de cuerpo libre.
Por favor click aquí y siga el siguiente link para acceder al laboratorio virtual.
La clase continúa con la comprensión de una habilidad más que debe estar en tu caja de herramientas: Elaboración de diagramas de cuerpo libre.
https://www.fisicalinda.com/courses/la-caja-de-herramientas/lessons/diagrama-de-cuerpo-libre/
Por favor, primero estudia ese tema para poder continuar comprendiendo lo que sigue:
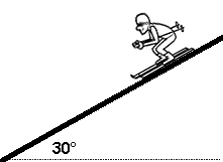
Ejemplo 5) ¿Cuál es la aceleración de un esquiador de 70 kg que baja una pendiente de 30°, si está resbalando sobre el plano inclinado con μ =0,07 y ha partido del reposo?
Guía para resolverlo: Nota: video que lo explica al final.
| A) Primero observe la figura que representa el problema: |
|
|
| B) Segundo: Construya un diagrama de cuerpo libre (es una representación de las fuerzas simplificado al máximo), el diagrama es el de la derecha, el del centro es solo para que te ubiques. | 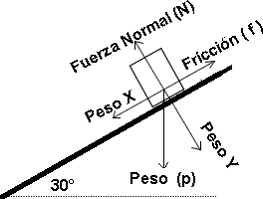 |
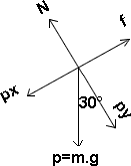 |
- C) Tercero: Resuelva.
- Respuesta:Piden aceleración, por lo tanto, parto de la fórmula general:
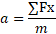 El problema ahora es que no tengo la ∑F que ocupo.Parece que el cuerpo se acelera entre el eje X y el eje Y, de modo que parece que habría que calcular el vector aceleración en X y luego en Y para al final sumarlos vectorialmente, pero como veremos seguidamente la ∑Fy=0 por eso no es relevante la suma vectorial, de modo que:
El problema ahora es que no tengo la ∑F que ocupo.Parece que el cuerpo se acelera entre el eje X y el eje Y, de modo que parece que habría que calcular el vector aceleración en X y luego en Y para al final sumarlos vectorialmente, pero como veremos seguidamente la ∑Fy=0 por eso no es relevante la suma vectorial, de modo que: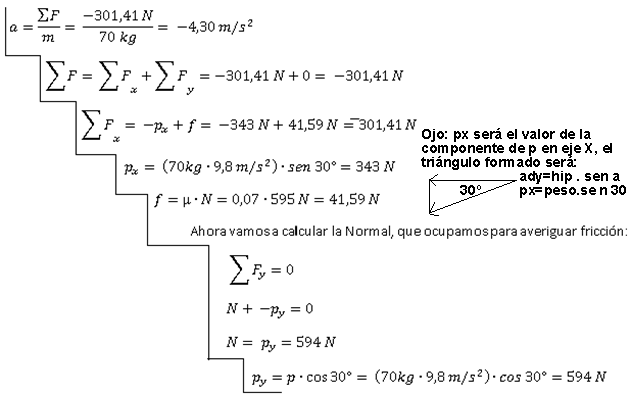 Nota: Hay otra solución (por demostración) de éste problema en la cual no se usa la masa.
Nota: Hay otra solución (por demostración) de éste problema en la cual no se usa la masa.
| Resumen:
Si quiere averiguar la aceleración de un cuerpo lo hará con a = F / m; pero si quieres averiguar la aceleración en el eje x de un cuerpo que es halado por varias fuerzas deberá usar ΣFx, por lo tanto, la fórmula será ahora a= ΣFx / m; recuerde que si le dicen que hay una fricción, la debe sustraer en el cálculo de la ΣFx. Otro aspecto a cuidarse es que cuando no le dan el valor de la fricción y sólo le dan el coeficiente de fricción (rozamiento), para poder calcular el valor de la fricción, debe averiguar la normal, para los siguientes problemas siempre parta de que hay equilibrio estático en Y, de modo que ΣFy = 0, esto es útil pues dependiendo de las fuerzas, plantee la ecuación de equilibrio incluyendo la normal y la despeja. Quizá en este punto esté preguntándose ¿Cuándo usar ΣFy y cuando ΣFx ? En los problemas que siguen todas las cajas se mueven en X, entonces debido a que medimos el ángulo respecto al eje x, la respuesta simple es: Para averiguar aceleración en X usa ΣFx lo cual implica calcular coseno. Para averiguar normal usa ΣFy lo cual implica calcular seno. |
En la solución de estas prácticas encontrarás una estrategia pedagógica desarrollada por el autor para solucionar los problemas extensos, permite ordenar los procesos, mejora la calidad y orden del estudiante. Consiste simplemente en ir escribiendo las fórmulas según vaya teniendo necesidad de usarlas, en diferentes escalones de la escalera, de modo que la primera fórmula será la de la incógnita del problema, y la incógnita de esta fórmula se resuelve con otra fórmula que se escribe en el siguiente escalón, y así sucesivamente; después se inicia la solución de abajo hacia arriba.
Por supuesto, queda a su elección usarla o no usarla, pero ayuda mucho para visualizar los errores de los alumnos y revisar el desarrollo en los exámenes, y a los alumnos les ayuda pues es una forma visual de identificar los procesos a seguir.
En los siguientes ejemplos se le pedirá la aceleración, recuerde que F= m.a.
El siguiente simulador virtual te permitirá comprender mejor lo explicado, ahora trabaje las actividades con fricción:
Favor da click aquí para acceder al simulador.
1) Cuál es la aceleración de la siguiente caja si hay una fuerza de rozamiento cinético de 10 N.
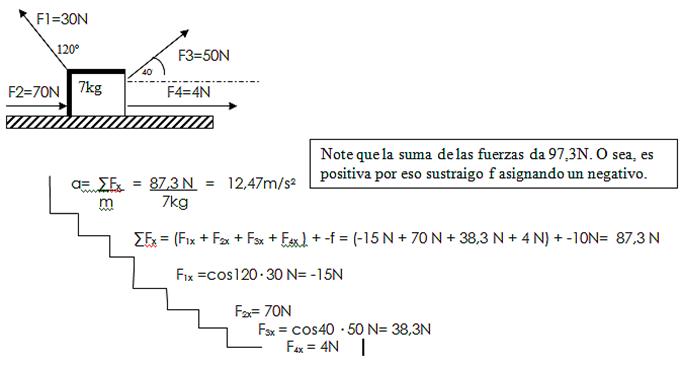
2) Cuál es la aceleración de la siguiente caja si hay un coeficiente de rozamiento cinético de 0,06.
No te asustes con estos problemas, generalmente a mis alumnos este tema les es uno de los más fáciles, llega a convertirse en algo mecánico, ya verás cuando hagas práctica y le agarres el volado qué fácil que es.
Práctica de Segunda Ley de Newton.
Resolución de problemas: Responda correctamente lo que se le solicite.
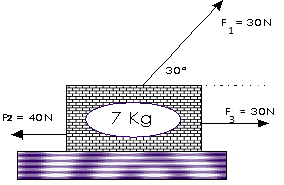
1) a) ¿Cuál es la aceleración de esta caja, si hay una fricción con el piso de 15N al moverse? Dibuje la flecha que representa la fricción bajo la caja.
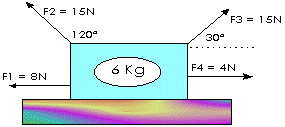
2) ¿Cuál es la aceleración de esta caja si hay una fuerza de rozamiento cinético de 4N? Dibuje la flecha que representa la fricción bajo la caja
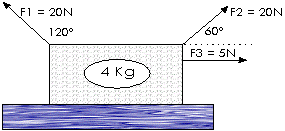
3) ¿Cuál es la aceleración de esta caja si hay una fricción de 5N? Rrepresente la flecha de la fricción bajo la caja.
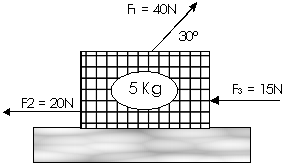
4) ¿Cuál es la aceleración de esta caja si entre ella y el piso hay un coeficiente de rozamiento de 0,25?
5) ¿Cuál es la aceleración de esta caja si entre ella y el piso hay un coeficiente de rozamiento de 0,8?
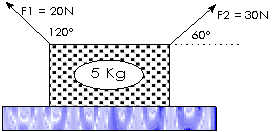
6) ¿Cuál es la aceleración de esta caja si está sobre un plano inclinado de 35° y la fricción es de 15N?
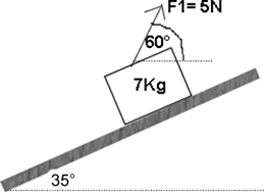
Puedes comprender mejor este problema viendo el diagrama de fuerzas aquí, simplemente adapte los datos:
Respuestas
1) 0,14m/s2
2) No se mueve pues SFx=1,49N y la fricción es mayor.
3) No se mueve, no hay flecha
4) No se mueve por que la fricción es mayor que la fuerza.
5) 0,088m/s2
6) 
Ejercicio final. Aplicación de conceptos en un sistema real.
Usando el mismo modelo del principio, averigüe la aceleración que tendrá la caja que se arrastra sobre las mesas. Para averiguar μk le servirá recordar que en términos generales para el caso de un cuerpo que se desliza sobre un plano inclinado, el μk se puede conocer a partir del momento exacto en que el cuerpo empieza a moverse mediante la relación μk = tan q donde q es el ángulo crítico de inclinación del plano en el exacto momento donde empezó a moverse (este vídeo le aclara cómo calcular el coheficiente de rozamiento):
.
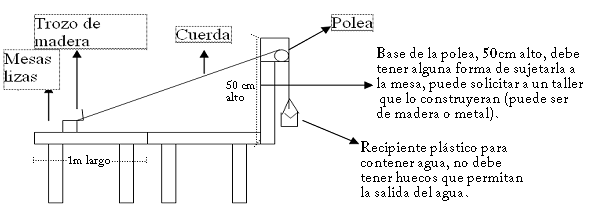
Si la masa colgada es cerca de 71g y la masa del trozo de madera es de unos 130g, es posible que el resultado de la aceleración sea cercano a 1,3 m/s2.
Nota: La solución de este ejercicio está en la guía del docente.
Sugerencia de Extraclase:
Objetivo: Aplica conceptos de Fuerzas a un caso real.
Proceso: En parejas diseñan una forma de calcular el valor de la fricción.
Averigüe la fuerza de fricción en esta situación:
Coloque una moneda en un extremo sobre una regla e incline la regla hasta el punto exacto donde la moneda empieza a moverse, en ese exacto punto usted puede predecir que el equilibrio estático de la fuerza que ejerce la gravedad (que usted puede calcular. Recuerde F=m.a) es la que acaba de vencer la fuerza de fricción, calcule el valor de dicha fuerza de fricción. Le servirá recordar que en términos generales para el caso de un cuerpo que se desliza sobre un plano inclinado, el μk se puede conocer a partir del momento exacto en que el cuerpo empieza a moverse mediante la relación μk = tan q donde q es el ángulo crítico de inclinación del plano en el exacto momento donde empezó a moverse.
En la página web del Banco Central usted puede localizar la masa de cualquier moneda. Recuerde usar siempre unidades del S.I.
Con seguridad ocuparan también un transportador para medir el ángulo de inclinación de la regla en el instante en que se pone en movimiento la moneda.
Si lo usa, tenga cuidado de medir el ángulo correctamente usando para eso la línea guía del transportador.

Deberán videograbar la elaboración del experimento donde se vea a todos los integrantes participando, dicho video es privado y solo me lo presentaran a mí como evidencia de la participación de los integrantes.
Finalmente deben presentar el cálculo por escrito con los resultados obtenidos y el diagrama donde se representan las fuerzas y moneda del problema.
Evaluación:
3 pt el video como evidencia de participación y trabajo, el video solo me lo muestran en su cámara o su teléfono.
3 pt el diagrama del problema con las fuerzas representadas en él.
3 pt el cálculo escrito con los resultados obtenidos.
3 pt el resultado correcto del cálculo de la fuerza de fricción.
Total: 5pt = 5%.
Escala: 1pt lo presenta de forma deficiente.
2pt lo presenta con algunas carencias.
3pt es presentado de forma completa y con todo lo solicitado.
Práctica para examen de II Ley de Newton:
Nota: Recuerde que para acceder a esta práctica debe tener como mínimo una cuenta de usuario y haber visto completamente el vídeo del tema.