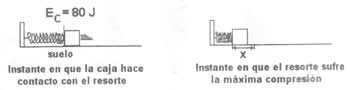
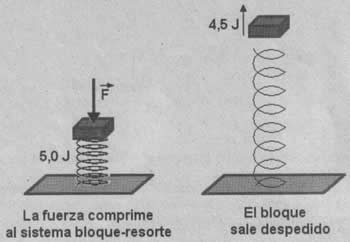
La Energía Mecánica
Energía Mecánica
Ahora relacionemos las dos energías estudiadas, la energía potencial y la energía cinética, pero ahora en el caso de una partícula que viene en caída libre desde cierta altura.
Recordemos que la energía potencial es la energía propia de los cuerpos en reposo, o sea que a medida que un cuerpo se empieza a mover su energía potencial se empieza a transformar en energía cinética. Un ejemplo que es muy útil para captar este concepto es este (lea Ep como Energía potencial y Ec como energía cinética.):
Si sostengo una bolita en un lugar alto y no la he soltado, por lo tanto, podemos decir que: Ec=0 J y Ep=10 J.
Ahora soltamos la bolita, la cual cae en caída libre; entonces la Ep empieza a transformarse en Ec, de modo que al aumentar la velocidad veré como sucede algo así desde que parte del punto de reposo en lo alto:
Ec= 0 J y Ep= 10 J.
Ec= 1 J y Ep = 9J
Ec= 2 J y Ep= 8 J
Ec=10 J y Ep= 0 J
¿Puede existir el caso donde Ec=11 J y Ep=0 J ?
Creo que respondiste bien, ¡NO! debido a que las leyes de conservación de la energía exigen que la suma de las dos energías (cinética más potencial) sea igual en todo momento, y dicho sea de paso, a la suma de las dos energías se le denomina Energía Mecánica:
EM = Ec + Ep
Esta ley se cumple ÚNICAMENTE cuando hay fuerzas conservativas porque en el caso de fuerzas disipativas la energía inicial es mayor que la final.
Entonces ahora podemos decir que la energía siempre es constante, de esta forma:
Energía Mecánica inicial = Energía Mecánica final
EMi = EMf
Pero como energía mecánica es la suma de la energía cinética más la potencial, puedo decir:
Ecinicial + Epinicial = Ecfinal + Epfinal
o sea
![]()
El anterior enunciado es válido en casos en que no se pierda la energía por fricción o calor y se llama: Ley de la conservación de la Energía Mecánica.
Piense en esta situación:
Se deja caer libremente un cuerpo desde el reposo.
Analice el siguiente gráfico del descenso del cuerpo:
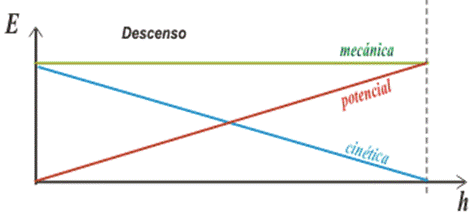
Explique por qué las curvas de energía potencial y cinética son invertidas y por qué la de energía mecánica es horizontal.
__________________________________________________________________________________
__________________________________________________________________________________
Puede ver la siguiente animación que ayuda a entender el tema, por ahora elija la opción Introducción:
Procure que los alumnos trabajen sin fricción y cambien el tamaño de la masa y que observen el resultado, de ese modo podemos confirmar lo visto en caída libre, que el valor de la masa no afecta la velocidad de llegada, ni el tiempo de caída.
Otra vez tenemos oportunidad de ejercitarnos
Práctica
1) ¿Cuánta es la energía potencial de un saco de 100kg puesto a 3m de altura?
2) Se deja caer una piedra de 8 kg de un edificio de 30m, calcule la energía cinética y potencial en los siguientes puntos:
Nota: Éste es un problema típico que se resuelve fácilmente con Ley de Conservación de energía mecánica.
- a) En el punto de partida.
- b) A 15 m de altura. Recuerde
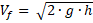 pero si usa esa fórmula llegará al mismo resultado que los que lo solucionan por lógica.
pero si usa esa fórmula llegará al mismo resultado que los que lo solucionan por lógica.
- c) En el momento en que llega al suelo.
- d) Calcule la energía mecánica en los tres puntos anteriores.
Nota: La energía mecánica siempre es constante si no hay fuerzas disipativas en el sistema (fricción).
Respuestas
| 1) 2 940J
2) A) Ec=0J Ep=2 352 J B) Ec=1175.11 Ep=1176J Observe la suma de la Ec y la Ep siempre es constante. Esto es energía mecánica. C) Ec=2352J Ep=0 D) En a E.M= 2352 J En b E.M= 2352 J En c E.M= 2352 J |
Ampliación del concepto de Fuerzas conservativas y Fuerzas no conservativas
Recuerde que cuando la fuerza es uniforme se puede afirmar que W= F.d , y si la fuerza que empuja al cuerpo no experimenta fricción, la energía mecánica inicial es igual que la final (EMi = EMf); pero, en otros casos la fuerza aplicada experimenta pérdida, por ello el trabajo se dice que es dado por fuerzas disipativas, donde hay pérdida de energía mecánica, de modo que la energía mecánica inicial es mayor que la final, en otras palabras:
- a) Fuerzas conservativas: Son aquellas donde el valor del trabajo hecho no depende de la trayectoria seguida sino únicamente de la posición inicial y final, de modo que
EMi =EMf
Ejemplos de fuerzas conservativas son: la fuerza gravitatoria y la fuerza elástica.
- b) Fuerzas No conservativas o disipativas: Son aquellas donde el valor del trabajo depende de la trayectoria del objeto sobre el que actúa, de modo que
EMi>EMf
Y para calcular la energía mecánica final debemos conocer:
EMf = Wfuerzas conservativas + Wfuerzas no conservativas
El más claro ejemplo de estas fuerzas son las fuerzas de fricción, entre más se desplace en su trayecto entre la posición inicial y final, más trabajo harán estas fuerzas. Como su nombre lo indica disipan la energía mecánica total del sistema.
Antes de empezar la práctica elabore un Mapa Conceptual que resuma todo el tema de Trabajo y Energía, en el mapa conceptual agregará además fórmulas y unidades.
Práctica para examen de Energía Cinética y Potencial
Práctica para examen de energía cinética, potencial y mecánica
Práctica final de todo el tema de trabajo y energía
Nota: Elabore un anexo con los análisis dimensionales de cada fórmula aplicada.
Primeramente, hagamos los despejes para obtener las fórmulas que usarán en algunos problemas.
1) De la siguiente ecuación
![]()
Despeje: a) V2
Le ayudaré con este despeje:
Como se busca la V de la fórmula el primer paso es meter los paréntesis e identificar la incógnita:
![]()
Ahora entonces paso m.g.hf a restar al otro lado
![]()
paso el 2 a multiplicar
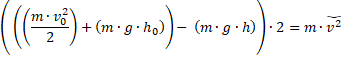
paso la m a dividir
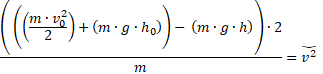
Si notas, la m está como factor común de todos los términos del lado derecho, por eso la puedo sacar y así eliminar una m arriba con una m abajo, así:
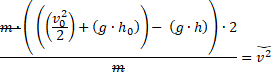
Entonces obtenemos
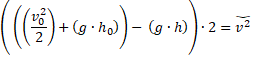
Y podemos eliminar paréntesis para que se vea más simple, quedando así:
![]()
Ahora elabore los siguientes despejes
| a) V02
|
| b) hi
|
| c) hf
|
2) En la cima de una montaña rusa a 25 m de altura, un carrito tiene una velocidad de 1 m/s, calcule la velocidad a los 10 m y 18 m y 0 m de altura.
3) Un objeto a 50 m de altura sobre el suelo posee una energía potencial de 34 300 J ¿Cuál es la masa de este objeto?
4) En el momento que un ciclista se desplaza a 10 m/s y su energía cinética es
3 500 J, aplica los frenos hasta detenerse. ¿Cuál es el trabajo realizado para que se detenga el ciclista?
5) Un vagón se desplaza horizontalmente y en cierto momento su energía cinética es 50 000 J. Si posteriormente su energía cinética aumentó a 75 000 J en un pequeño trayecto, ¿cuál fue el trabajo realizado por la fuerza encargada de aumentar su energía cinética?
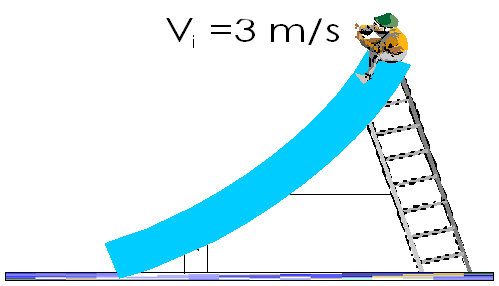
6) Desde la parte superior de un tobogán de 15 m de alto , se impulsa una persona con una rapidez de 3,0 m/s. Suponiendo la fricción despreciable calculemos:
Nota: Resolverlo con Ley de Conservación Energía Mecánica.
- a) La rapidez cuando la persona está a 0,5m del suelo.
- b) La altura a la cual va la persona cuando ha alcanzado una rapidez igual al doble de la inicial.
7) Investigue cómo se averigua la cantidad de energía desprendida por un temblor, ocasionada por los volcanes o bien por movimiento de placas tectónicas, puede indagar en la página web del OVSICORI o en otras, buscando información relevante para su investigación.
Finalmente relacione sus conclusiones con trabajo y energía.
Resuelva este crucigrama:
Aplicación:
Usando el mismo modelo que hemos usado en el tema de fuerzas:
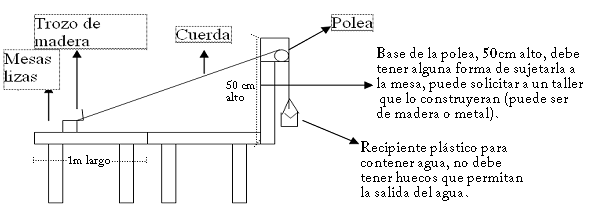
Ahora averigue el trabajo total del sistema:
- Usando la formula general de trabajo.
- Usando energías (tome en cuenta que existe fricción)
Práctica de profundización:
Selección única: Marque con una equis la respuesta correcta bajo cada encabezado.
8) Si la velocidad de un objeto se reduce a la mitad, su nueva energía cinética, comparada con la anterior será:
- a) mitad
- b) cuatro veces
- c) la cuarta parte
- d) la octava parte
9) Desde cierta altura a partir del suelo, un objeto cae libremente y su energía potencial disminuye y a la vez, la energía
- a) cinética aumenta
- b) cinética disminuye
- c) mecánica aumenta
- d) mecánica disminuye
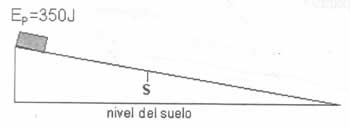
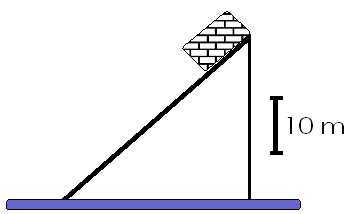
10) Una caja está a 10 m de altura en un plano inclinado sin fricción, como muestra la figura, y empieza desde esa posición a desplazarse desde el reposo. Cuando llega al pie del plano, tiene una velocidad cuya magnitud es:
| a) 10 m/s
b) 14 m/s c) 98 m/s d) 196 m/s |
 |
11) Aquellas situaciones físicas en las que la energía mecánica se conserva, se caracterizan porque intervienen exclusivamente fuerzas
- a) conservativas
- b) constantes
- c) disipativas
- d) variables
12) ¿Cuál es el trabajo mínimo para subir un barril que pesa 45N, hasta una altura de 5m?
- a) 225 J
- b) 0.1J
- c) 45J
- d) 9
13) Una fuerza horizontal de 30N logra desplazar un cajón sobre el piso horizontal, 5m. El roce con el piso hace aparecer una fuerza de fricción de 5N a lo largo de esa distancia, el trabajo de la fuerza resultante en ese tramo es
- a) 175J
- b) 150J
- c) 125J
- d) 25J
14) Un cuerpo cae libremente después de soltarse de cierta altura. Si la masa de ese cuerpo es 2kg y llega al suelo con velocidad de 30m/s, el trabajo de la fuerza gravitacional sobre el cuerpo es de
- a) 1800J
- b) 900J
- c) 588J
- d) 60J
15) Se dice que intervienen fuerzas disipativas cuando el trabajo de esas fuerzas sobre un cuerpo
| a) permite que la energía mecánica se conserve b) permite que la energía cinética se conserve |
c) no depende de la trayectoria. d) depende de la trayectoria. |
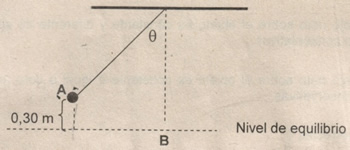
16) La masa de un péndulo está a 0,2 m de altura respecto al punto más bajo. Si es Suelta desde esa altura, la velocidad al pasar por el punto más bajo es
- a) 9,80m/s
- b) 3,92m/s
- c) 1,98m/s
- d) 0,99m/s
17) Observe la figura
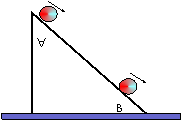 |
Si la pelota inicia su movimiento en A con velocidad Va.
y al pasar por b, se mueve con velocidad Vb. Y no actúan fuerzas de rozamiento, se puede afirmar que la energía
|
- a) mecánica al pasar por el punto B, es igual a la suma de las energía cinética y potencial en el punto A.
- b) potencial al pasar por el punto B, es el doble de la energía potencial en el punto A.
- c) potencial en el punto A, es igual a la energía potencial en el punto B.
- d) cinética de la bola al pasar por B, es igual a cero.
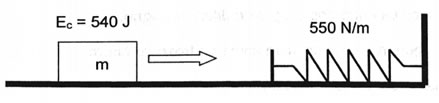
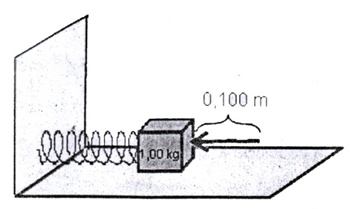
18) Un bloque de 2kg comprime un resorte de constante elástica 40N/m. Cuando el resorte se suelta, empuja al bloque sobre una superficie horizontal sin fricción, y el bloque se separa con rapidez 0,5m/s. Antes de soltarse está comprimido a una distancia de
- a) 0,16m
- b) 0.11m
- c) 0.02m
- d) 0.01m
Respuestas:
| 2)10m: 17 m/ 18m: 11,7 m/s 0m: 22 m/s 3) 70 kg 4)W= ΔEc = 0- 3500J= – 3500 J 5) 25 000J |
6) a)17.12 m/s
b) 13,62 m 7) Es investigación 8)c 9)a
|
10)b
11)a 12) a 13)c
|
14) b
15)d 16)c 17) a 18)b
|
Práctica final para examen sobre el tema de Trabajo y Energía:
Nota: recuerde que para acceder a la práctica primero debe estar registrado como usuario y haber visto completamente el vídeo del tema.