Movimiento Rectilíneo y Uniforme (M.R.U.)

El vídeo anterior debe verlo completo para que se le asigne progreso. El vídeo que sigue abajo es lo mismo pero explicado en una clase, si usted entendió con el primero NO es necesario que vea este segundo vídeo:

¿Por qué es útil estudiar el movimiento?

Nota para el docente: Por favor considere la siguiente idea para el tema de conversiones:

https://www.fisicalinda.com/lessons/didactica-para-abarcar-conversiones/ 

¿Habría más accidentes de tránsito si los vehículos no tuvieran velocímetro?

_______________________________________________________________

El velocímetro nos ayuda a decidir si disminuir la velocidad cuando transitamos donde está mojada la calle, nos ayuda a medir hasta el tiempo que duramos en llegar a un lugar. Y la existencia del velocímetro no sería posible si nadie hubiera estudiado el movimiento, así es que, ¡entendamos estos principios!

El estudio del movimiento se remonta desde antes de 384 a.E.C. cuando Aristóteles se pregunta cuál era la causa del movimiento, hasta 1590 cuando Galileo Galilei explica que el movimiento es causado por alguna fuerza y una vez suspendida la fuerza el cuerpo sigue moviéndose; de no existir otra fuerza que lo frene. En la actualidad a esto se le denomina movimiento rectilíneo y uniforme (M. R. U.).

MRU significa Movimiento Rectilíneo (en línea recta) y Uniforme (a velocidad constante).

Distancia y desplazamiento

También cuando un cuerpo se mueve, el camino que sigue desde la posición inicial hasta la posición final se denomina “distancia” y es un escalar; pero, a la longitud (en línea recta) desde la posición inicial a final, se le denomina “desplazamiento” y es un vector.

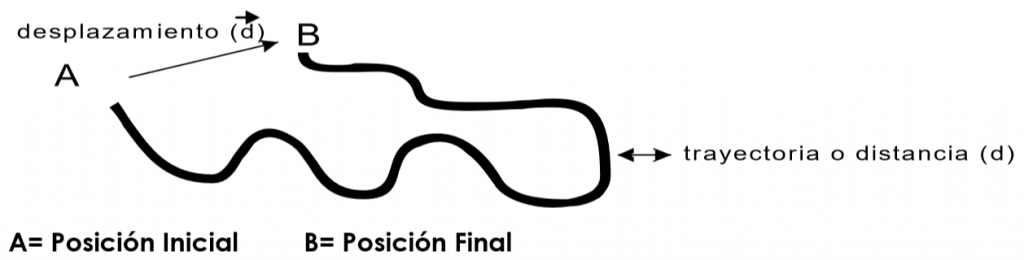
En las prácticas y para no complicar más la vida de lo necesario, sé, por experiencia, que la forma más fácil de averiguar un desplazamiento es simplemente verlo en el dibujo, para ello:

1) Localice la posición inicial y la posición final

2) Entonces trace una recta entre ambas

3) Lo que mida esa recta es el desplazamiento y hacia dónde va, es la dirección.

Ejemplos: ¿Cuál es el desplazamiento y la distancia en los siguientes casos?

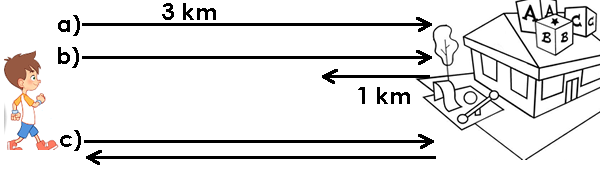
a) Salgo de mi casa y recorro 3 km al norte hasta el colegio.

b) Salgo de mi casa y recorro 3 km al norte hasta el colegio y regreso 1 km al sur.

c) Salgo de mi casa y recorro 3 km al norte hasta el colegio y regreso hasta mi casa.

[h5p id=”4″]

Velocidad y rapidez

Generalmente usamos los términos velocidad y rapidez sin hacer distinción entre ellos, hoy aprenderemos que son diferentes, ambos términos no son lo mismo, velocidad es un “vector” por lo tanto tiene dirección.

Ejemplo 60km/h al norte, 3m/s al suroeste. Pero la rapidez es un escalar o sea sólo el número, de modo que 60km/h, 3m/s serán la rapidez.

Pero la rapidez es un escalar o sea sólo el número, de modo que 60km/h, 3m/s serán la rapidez.

Video que aclara detalles sobre la diferencia entre rapidez y velocidad:

Y los términos diferentes que hemos aprendido se relacionan de la siguiente forma:

Donde significa cambio y siempre este símbolo significa cantidad final menos cantidad inicial.

Aquí hablamos de velocidad y de rapidez media, conceptualmente esto es diferente de velocidad o rapidez instantánea.

Velocidad o rapidez media: Es la que obtenemos a partir de cálculos donde usamos dos valores de tiempo o distancia, es un promedio de velocidad o rapidez en cierto lapso.

Velocidad o rapidez Instantánea: Es la que mide el velocímetro de los carros o la que los tráficos miden con sus “radares” (esas “pistolas” para medir la velocidad, se llaman técnicamente pistola Doppler).

RESUMEN:

Distancia: (d)es la longitud del camino que sigue desde la posición inicial hasta la posición final, es un escalar, ejemplo: 30m, 15 km, 25cm.
Desplazamiento: (  ) es la distancia mínima (en línea recta) dirigida desde la posición inicial a la posición final, es un vector, ejemplo: 30m al sur, 15 km a la derecha, 25 cm hacia arriba.

Generalmente para averiguarlo no necesitan calcularla sino solo verla en el dibujo buscando posición inicial y final y tirando una recta entre ambas.
Velocidad media:  

Es un vector, ejemplos: 10m/s al sur, 60 km/h hacia delante, 18 m/s hacia abajo.
Rapidez media:  

Es un escalar, ejemplos: 10m/s, 60 km/h, 18 m/s.

Pero durante este curso solamente averiguaremos la velocidad y la rapidez instantánea, por eso usaremos las fórmulas sin la m.

 PRIMERAS NOCIONES DE DESPEJE

El siguiente video explica de forma simple como hacer despejes y además cómo resolver problemas de MRU.

Algo muy importante es aprender a despejar y a través de todo este curso de Física usted aprenderá bastante, y empecemos a despejar desde hoy con esta primera fórmula:

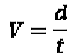
Despejar significa dejar de un lado la variable que quiero, no importa si la deja sola del lado derecho o izquierdo, lo que importa es dejarla sola, si queda del lado derecho simplemente la traslada a la izquierda sin cambiar nada.

Para despejar; lo último que usted mueve es la variable a despejar, lo que le piden, y lo principal que debe recordar es que al pasar al otro lado del igual solamente se cambia de operación, o sea, si está sumando pasa a restar, si está restando a sumar, si está multiplicando a dividir y si está dividiendo a multiplicar, apliquémoslo.

Despeje distancia de la siguiente fórmula:

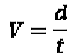
para hacerlo observe que la variable “tiempo” es lo que debe pasar al otro lado entonces páselo, note que está dividiendo, por ello pasa a multiplicar

Y como d quedó a la derecha la podemos pasar; sin hacer ningún otro cambio; a la izquierda

Ahora despejemos tiempo de

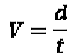
En los casos donde la incógnita esté en el denominador (lo que busca está abajo), la mejor y más simple forma de despejarla es trasladar la variable incógnita al lado izquierdo y la que está al lado izquierdo del igual, es trasladada al lado derecho; de modo que t va a la izquierda arriba y V para abajo.

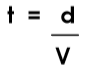
Otro modo muy usado de iniciarse en el despeje y que se puede usar con cualquier fórmula con tres variables es usar el triángulo, poniendo la variable de arriba en la parte superior, la de la izquierda a la izquierda y la otra a la derecha, tal como se ve en la imagen.

Su profesor indicará cómo usar este triángulo.

¿CÓMO RESOLVER PROBLEMAS DE MRU?

1) Elabore un dibujo exacto que describa el problema y anote los datos en él.

2) Saque los datos del problema. Ejm, d=3m, t=2s ,V=?

3) Busque la fórmula que responda la pregunta del problema.

4) Sustituya en la fórmula con los datos (no olvide escribir las unidades. Ejm V=d/t = 3m/2s=)

5) Escriba la respuesta con las unidades correspondientes. Ejm V= 1,5 m/s

6) Si en algún problema aparecen datos en m y km, o m/s y km/h, deberá hacer la conversión correspondiente para siempre trabajar en unidades homogéneas.

Ahora continuemos con el tema en la resolución de prácticas, los siguientes ejemplos están resueltos, por favor en la solución de la práctica siga el proceso que se describe aquí:

Ejemplos:

1) ¿Cuál es la velocidad media y el desplazamiento de un carro que está a 400m a la derecha de un árbol y después de 5s está a 100m a la izquierda del mismo árbol?

Puntos a calificar: 1pt datos correctos, 1pt dibujo con datos correctos, 1pt fórmula correcta, 1pt sustitución correcta, 1pt resultado correcto: Total: 5pt

Datos: Posición inicial = 400m a la derecha del origen.

Posición final = 100m a la izquierda del origen

t = 5s

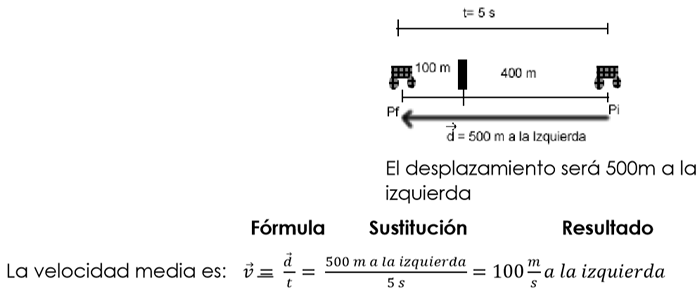
OJO: La sustitución debe tener las unidades, si no tiene unidades y dirección, pierde el punto.

2) ¿Cuál es la velocidad en m/s media de un carro que recorre 30km en 2 horas; si se dirige hacia el norte?

1pt datos correctos, 1pt fórmula correcta, 1pt sustitución correcta, 1pt resultado correcto. Tot: 4pt

Ya obtuvimos esta velocidad en km/h, pero el problema la pide en m/s, así es que hay que hacer la conversión.

Recordemos conversiones:
Quiero convertir 15 km/h a m/s

Por lo tanto, la respuesta del problema es: 4,16 m/s al Norte

Si no recuerdas conversiones, te recomiendo que descargues y por tu propia cuenta estudies el tema de conversiones:

https://www.fisicalinda.com/lessons/conversiones/

Práctica.

Nota: si vale 5pt, estrictamente requiere un dibujo para su solución.

1) Un perro está a 150 m sur de un árbol de mango; entonces, su dueño lo llama y el perro empieza a caminar hacia el árbol, dura 2 minutos caminando cuando se echa a descansar al lado del árbol ¿A qué velocidad en m/s caminó el perro hacia el árbol? 5pt

Solución:

2) Un río cuya rapidez es 10 m/s trae una hoja, la cual dura 2min en llegar al puente, ¿Cuánta distancia recorrió? 4pt

Solución

3) Un avión recorre 5 000 km al norte en 3 días, ¿cuál es su velocidad en km/h? 4pt.

Solución:

4) Una bicicleta baja del Cerro de la Muerte durante 15 min a 40 km/h, ¿Cuánta distancia recorre? 4pt.

Solución:

5) Un pájaro vuela a 2 m/s y recorre 10 hm, ¿cuánto tiempo duró? 4pt.

6) Un cuervo sale de su nido y vuela 30m hacia el roble, 10 minutos después regresa al nido, averigüe el desplazamiento y la distancia. 5pt.

7) A José Palito su mamá lo envió a la pulpería a comprar arroz, si él estaba en la esquina del mercado cuando lo enviaron, de acuerdo al dibujo siguiente, recorrió 100 m este hacia la escuela, entonces dobló 300 m sur hasta llegar a la pulpería:

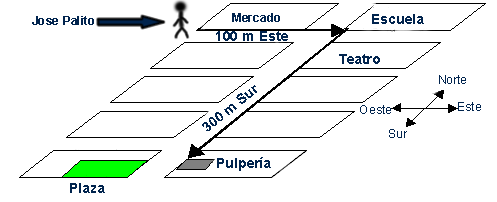
Si tardó 9,50 minutos, ¿A cuál velocidad en m/s caminó José Palito?

8) Un chompipe está a 50 m norte del colegio y dura 20 segundos en estar a 10 m norte del colegio; entonces, 30segundos después está a 30m sur del colegio, calcule: (1pt elaboración del dibujo, 11pt en cada proceso y resultado correcto) a) distancia total recorrida

b) desplazamiento total recorrido

c) distancia al norte recorrida

d) desplazamiento al norte recorrido

e) desplazamiento al sur recorrido

f) distancia al sur recorrida

g) velocidad media al norte

h) velocidad media al sur

i) rapidez media al norte

J) rapidez media al sur

9) Una abeja sale de su panal y recorre 15 m a 45°, luego 10 m a 280° y finalmente 30 m a 70°. En todo el viaje duró 800 segundos. Averigüe la velocidad promedio en m/s en que se movió y la rapidez promedio. (2pt sumas de componentes correctas, 2pt vectores y escalares correctos, 2pt fórmulas correctas, 2pt sustituciones correctas, 2pt respuestas correctas. Total: 10pt)    Video que lo explica:

	Valor en eje X	Valor en eje Y
	10,60	10,60
	1,73	-9,84
	10,26	28,19
Suma total	22,59	28,95

9) Con el conocimiento adquirido, por favor corrija este rótulo de carretera, dibújalo al lado con todas las correcciones.

Ahora imagina que vas en un automóvil cuyo velocímetro es el siguiente, ¿dónde debería estar la aguja para que su rapidez sea exactamente la máxima permitida según el anterior rótulo?

EXPERIMENTO DE REAFIRMACIÓN DE CONOCIMIENTOS MRU.

Vamos a comprobar lo que hemos visto en teoría con el caso de la rapidez:

1. Descargan una app gratuita para medir rapidez de un cuerpo en movimiento hacia la cámara, por ejemplo, Radar de Velocidad (Speed Gun). Tenga cuidado de que no descargue una app para medir “velocidad de descarga” de bytes en Internet o una que mida la “velocidad” propia del cuerpo.

2. Marque una distancia conocida y corta, unos 20 m será suficiente y midan el tiempo en que un compañero recorre dicha distancia corriendo a “rapidez” constante, luego calcule la rapidez.

La rapidez corresponde a: ___________________

3. En el mismo momento, el alumno que descargó la app mida la rapidez registrada en el teléfono con la app. 4. ¿Hay diferencia en los resultados? en caso afirmativo, ¿cuáles podrían ser algunas razones? ¿Están obteniendo el resultado en la misma unidad? _________________________________________________________________________________
_________________________________________________________________________________.

Seguidamente encontrará la práctica final de MRU, pero si ya estás a punto de presentar la prueba (examen) de MRU, es muy apropiado que veas el siguiente video: