La tensión
Tensiones
Cuando dos cuerpos físicos están en contacto, la fuerza entre ellos puede tener distintos nombres (por ejemplo, ya habíamos visto anteriormente la definición de normal), pero cuando la fuerza es hecha por una cuerda, cable, cadena o hilo, a esa fuerza se le llama tensión.
La tensión es la fuerza con que se tira de una cuerda o cable que está tenso, y por tercera ley de Newton, en cada extremo de la cuerda dicha fuerza tiene sentidos opuestos. Entonces, la tensión es una fuerza.
Además se parte del supuesto de que las cuerdas tienen masa despreciable y son indeformables, claro en la vida real esto no se cumple, pero para efectos prácticos de este tema, debemos partir de esos supuestos.
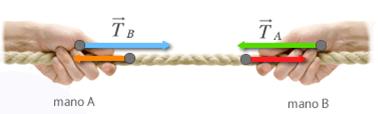
Créditos de imagen: www.fisicalab.com
Interpretemos con cautela la imagen: La fuerza de la mano A es hacia la izquierda y por tanto genera una tensión en la mano B que va hacia la izquierda. De igual forma, la fuerza de la mano B es hacia la derecha y genera una tensión en la mano A que va hacia la derecha.
De modo que se puede establecer que:
![]()
Recuerde que trabajamos con cuerdas y la tensión es una “fuerza de tracción”, eso significa que sirve para jalar, no para empujar, eso parece obvio, pero cuando se hacen dibujos de fuerzas o diagramas de cuerpo libre, parece que lo olvidamos y algunas veces interpretamos que la fuerza de tensión está empujando.
No hay una sola fórmula para calcular la tensión pues todos los problemas son diferentes y las tensiones son diferentes, por eso, igual que con el caso de la normal, no existe una sola fórmula sino que tenemos que sacarla a partir de condiciones de equilibrio, partiendo siempre de que:
![]()
![]()
Veamos un ejemplo y su método de solución:
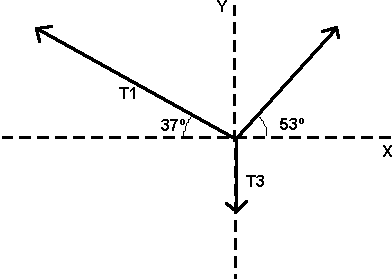
1) Un semáforo que pesa 100 N se sostiene por un cable que está atado a otros dos que, a su vez, están sujetos a un soporte, como se muestra en el dibujo. Los cables superiores forman ángulos de 37º y 53º con la horizontal, respectivamente. Averigüe la tensión en cada cable.
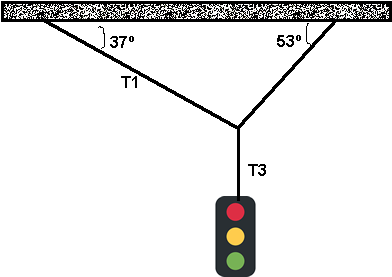 |
Solución
Para resolverlo sigamos varios pasos: 1) Construya el diagrama de cuerpo libre.
|
- 2) Como observamos el cuerpo no se mueve ni en X ni en Y, por tanto está en equilibrio estático.
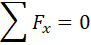
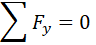
- 3) Ahora descomponemos cada sumatoria en sus términos e igualamos a cero, para luego despejar y averiguar cada tensión.
(1) ![]()
(2)![]()
Ahora trabajo la ecuación (1)
![]()
Despejo T2 obteniendo:
![]()
![]()
Ahora este valor de T2 se sustituye en la ecuación (2)
Ecuación (2) original:
![]()
Ecuación (2) sustituida:
![]()
![]()
Resuelvo y despejo T1 :
![]()
![]()
![]()
![]()
![]()
T1 = 60 N
Ahora como arriba habíamos encontrado que T2 = 1.33 T1 entonces:
T2 = 1.33 . 60 N = 79.8 N
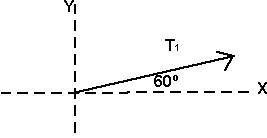
2) Una caja 2 kg está siendo arrastrada en el piso por una persona con una cuerda y la cuerda forma un ángulo de θ=60º con la horizontal, como se muestra en el dibujo. La tensión de la cuerda causa que la caja se deslice a través de la mesa hacia la derecha en una superficie sin fricción, con una aceleración de 3 m/s2. ¿Cuál es la tensión de esa cuerda?
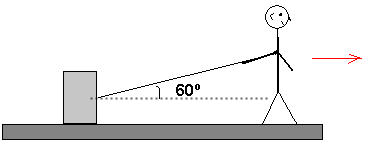 |
Solución
1) Este caso es tan simple que casi no ocupa diagrama de cuerpo libre, pero no importa, iniciemos con el diagrama de cuerpo libre para identificar las fuerzas:
|
2) Observamos que el único movimiento del cuerpo es hacia la derecha, por tanto la tensión estará en la suma de fuerzas en X:
∑Fx = T1 . cos 60° = 0
- Como la caja se mueve con aceleración, podemos sustituir en la fórmula de aceleración con los datos que tenemos:
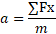
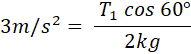
Despejo T1
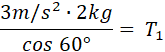
T1 = 12 N
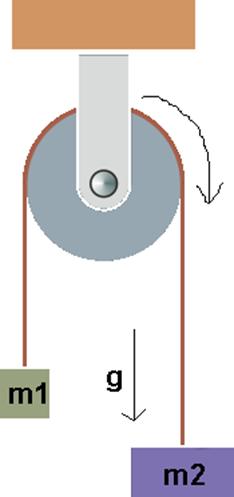
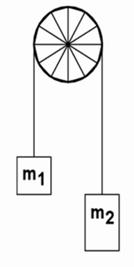
3) Máquina de Atwood:
Cuando colgamos dos masas verticalmente sobre una polea sin rozamiento, se obtiene lo que se llama máquina de Atwood, la cual puede ser usada para medir la aceleración de la gravedad.
Observe la imagen siguiente y averigüe la aceleración de las dos masas y la tensión en la cuerda.
 |
Solución
Por la imagen se ve que la m2 pesa más y va hacia abajo, mientras m1 va hacia arriba. Note, que esto se puede entender como una simple cuerda horizontal con dos masas que son fuerzas opuestas:
Al aplicar la segunda ley de Newton para m1 y m2 obtengo:
|
Como son dos masas en el sistema la aceleración se da por su suma
![]()
Ahora despejo aceleración y obtengo:
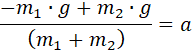
Una presentación más elegante pero igualmente funcional es si factorizamos gravedad:
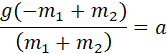
Ahora vamos a averiguar la tensión en las cuerdas, note que la tensión es una misma, la polea no afecta, de modo que podemos decir:
![]()
![]()
Despejo tensión: ![]()
![]()
Factorizo m1 y obtengo la tensión:
![]()
Práctica
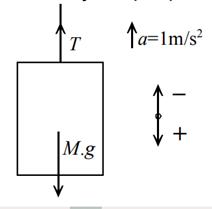
1) Un ascensor que pesa 8 toneladas tiene una aceleración de 1 m/s2. Calcule:
- a) La tensión del cable que lo sostiene.
- b) La fuerza vertical que el ascensor ejerce sobre una persona de 80 kg que está viajando adentro.
2) Una máquina de Atwood tiene una masa m1 de 10kg y la otra masa m2 es de 8 kg, usando la fórmula de aceleración para la máquina de Atwood, anteriormente obtenida, averigüe la aceleración de las masas y la tensión en la cuerda.
3) Un cable eleva una masa m= 800 kg la tensión en el cable es de 12000 N
- a) ¿Cuál es la máxima aceleración con que se puede elevar?
- b) Si se eleva con una a= 2 m/s2 ¿qué tensión soporta el cable?
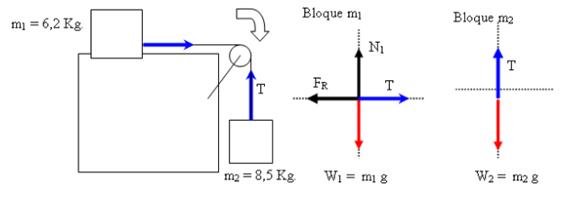
4) Un bloque de 8,5 kg que cuelga, se conecta por medio de un hilo de acero de masa despreciable, que pasa por una polea y llega a un bloque de 6,2 kg que se desliza sobre un bloque cuadrado liso, tal como se muestra en la imagen. Si el coeficiente de fricción durante el deslizamiento es 0,2, encuentre: La tensión en la cuerda.
5) Explique cómo podría ser útil el conocimiento de tensiones para evitar accidentes en estas máquinas:
¿Has visto algún video en redes sociales sobre accidentes relacionado con el mal uso de estas máquinas?
1) a) mg −T = ma
8000⋅9.8−T = 8000(−1)
T = 8000⋅10.8 = 86400 N
- b) mg − F = m.a F = m(g −a)
F =80[9.8−(−1)]=864 N
2) a= 1.09 m/s2 ; T= 108.9N
3) a) amax= 5.22 m/s2 b) T= 9440N
4) T = 42,16 N.
Solución:
∑Fy = = m1. a
∑Fy = = T – P1 = m1. a
T – m1 g = m1 a (Ecuación 1)
Bloque m2
∑Fx = m2. a
FX – T = m2 a (Ecuación 2)
Resolviendo las ecuaciones, encontramos la aceleración del sistema. (aquí sigo otro procedimiento un poco diferente del explicado arriba, pero el resultado es el mismo)
![]()
– m1 g + FX = m1 a + m2 a
a (m1 + m2 ) = – m1 g + FX
a (2 + 8) = -2 . 9,8 + FX
10 a + 19,6 = FX
Si a = 0
FX = 19,6 Newton, es decir es la mínima fuerza necesaria para que el cuerpo se mantenga en equilibrio.
Si a > 0 El cuerpo se desplaza hacia la derecha, por la acción de la fuerza FX
Para cuales valores de FX la tensión en la cuerda es cero.
Despejando la aceleración en la ecuación 1
T – m1 g = m1 a
T – 2g = 2 a![]()
Despejando la aceleración en la ecuación 2
FX – T = m2 a
FX – T = 8 a
![]()
Igualando las aceleraciones.
![]()
8 * (T – 2g) = 2 * (FX – T)
8T – 16g = 2FX – 2T
8T + 2T = 2FX + 16g
10T = 2FX + 16g
![]()
![]()
Si T = 0
![]()
FX = – 8 g