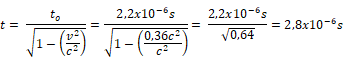Teoría especial de la relatividad:

En esta teoría básicamente trabaja con la I Ley de Newton, la ley de la Inercia, para ello Newton definió que todos los cuerpos inerciales moviéndose en sistemas conjuntos adquieren las velocidades correspondientes a la suma vectorial de sus vectores consecutivos. En palabras simples y con un ejemplo: Si vamos dentro de un bus a 20 m/s hacia adelante y yo tengo una bola en mis manos la cual impulso a 1m/s hacia adelante, esta bola viajará a 21m/s respecto a un observador en la calle.

Bueno, pues Einstein trabaja este mismo tema, pero ahora viéndolo desde la perspectiva de rayos de luz.

El caso es que Michelson y Moreley en 1887 habían realizado un experimento en el cual demostraron que la velocidad de la luz nunca cambia ( más información aquí: https://es.wikipedia.org/wiki/Experimento_de_Michelson_y_Morley ) y es fija de 300 000 m/s, por ejemplo, ellos encontraron que si tenemos un tren viajando a 200 000 m/s y alguien dentro del tren enciende un foco en la misma dirección del tren, la velocidad de ese rayo de luz para un observador afuera del tren no aumenta y sigue siendo de 300 000 m/s (Según Newton la velocidad de ese rayo de luz vista por el observador fuera del tren sería de 300 000 m/s + 200 000 m/s= 500 000 m/s).

Las explicaciones de Einstein tienen profundas implicaciones.

Con la teoría de la relatividad especial, la humanidad entendió que lo que hasta ahora había dado por sentado que era una constante, el tiempo, era en realidad una variable. No sólo eso, sino que el espacio también lo era y que ambos dependían, en una nueva concepción llamada espacio-tiempo.

La teoría especial se basa en dos conceptos:

• Principio de simetría de Lorentz (Hendrik Lorentz): Las leyes de la física son las mismas mientras se esté en un mismo sistema de referencia. En palabras simples: En un mismo laboratorio o tren se cumplen las mismas leyes si ambos se mueven a la misma velocidad.
• La velocidad fija de la luz descubierta por Michelson y Moreley en 1887: El postulado dice que la velocidad de la luz es fija, se denota como “c” y su valor es de 300 000 m/s según lo descubierto por Michelson y Moreley, independiente de todo movimiento relativo entre la fuente y el observador.

Ahora Einstein explica el fenómeno de la siguiente forma:

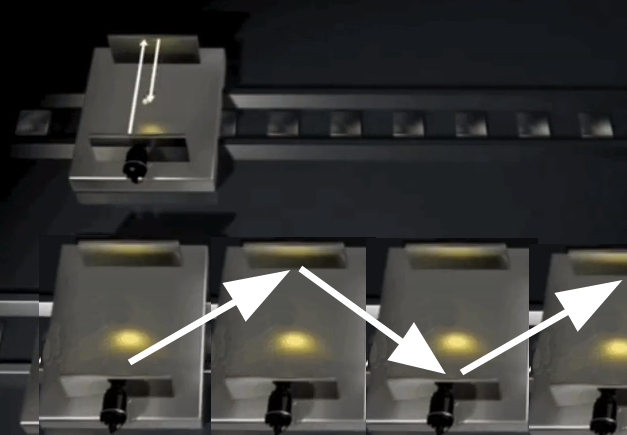
Imagine que la imagen de abajo son dos trenes que están en reposo, en las paredes de cada uno hay espejos y un fotón de luz es disparado entre los espejos, de modo que rebota en uno y otro, separadamente en cada tren en reposo:

Ahora el tren de abajo se pone en movimiento a alta velocidad. De modo que ahora la trayectoria seguida por el fotón para pegar en uno y otro espejo es más larga:

Para un observador adentro del tren de abajo, el tiempo que dura el fotón en llegar a cada espejo es el mismo que para un observador en el tren de arriba.
Pero para un observador afuera del sistema, como nosotros, el tiempo que tarda este fotón en ir de un lado a otro debe ser mayor porque la trayectoria que debe recorrer es mayor:

En el primer tren, en reposo, el tiempo que dura en recorrer esta distancia:

No es el mismo que el tiempo que dura en recorrer esta distancia que es levente más alargada:

Por esta razón se dice que a velocidades relativistas, cercanas a la velocidad de la luz, el tiempo se dilata (duran más las cosas, el tiempo se retarda).

Esto da pie a una paradoja llamada paradoja de los gemelos, expresada así:

Un gemelo a sus 20 años toma una nave espacial y va a conocer el universo viajando a la velocidad de la luz, 20 años después regresa a Tierra y al bajarse de su nave espacial saluda a su gemelo de 40 años, mientras que al bajar de la nave el baja con los mismos 20 años que subió.

Durante su viaje espacial su tiempo se retardó y ya que viajó a la velocidad de la luz, se detuvo respecto al tiempo en la Tierra.

Con un fuerte trabajo matemático y físico Einstein demuestra que:

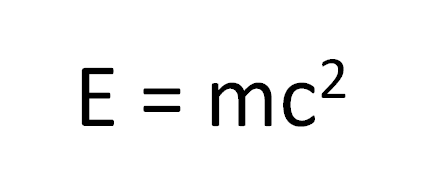
Esta ecuación en palabras simples indica que la energía de un cuerpo en reposo de un cuerpo corresponde a la multiplicación de su masa por la velocidad de la luz al cuadrado. Eso además significa que la masa y la energía son dos presentaciones del mismo fenómeno pero en diferentes estados, y tiene trascendencia en tres ámbitos:

Implicaciones científicas: Al comprender que la materia y la energía se pueden transformar uno en otro, da inicio a la carrera armamentista para construir una bomba que permita extraer la energía almacenada en los átomos, y posteriormente se construye la primer bomba de fusión atómica, con graves consecuencias al ser estrenada en humanos Hiroshima y posteriormente en Nagasaki. En dichas ciudades cuando la bomba explota, fue posible ver cerca de edificios la sombra de personas que fueron “evaporadas” debido al disparo de partículas que convirtieron su materia en energía. Nota: Einstein fue un  pacifista y se opuso completamente al desarrollo de la bomba atómica.

Implicaciones filosóficas: La masa es afectada por aspectos materiales y dimensionales del espacio-tiempo, pero la energía es por contraparte la misma sustancia pero en un estado tal que no es afectado por el espacio ni por el tiempo. Por eso existe una ley que dice que la energía no se crea ni se destruye, solo se transforma (no es afectada por el tiempo ni el espacio) pero no existe tal ley para la materia porque la materia si se puede crear y destruir, y también transformar, la materia si es afectada por el espacio y el tiempo.

Implicaciones Teológicas: Extrapolando esto a la teología podríamos explicar porque Dios no tiene principio ni fin si se entiende la esencia de Dios es energía, para quienes son cristianos puede ser interesante lo descrito en Isa 40:26 (la palabra original para poder ahí es energía). Donde aclara que Dios es energía dinámica (traducido poder en algunas biblias).

La dilatación del tiempo

Una de las consecuencias de la teoría especial de la relatividad es la dilatación del tiempo, esta puede calcularse con:

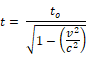
Donde t= tiempo relativo medido en el otro sistema, o sea el tiempo dilatado.
t₀= es el tiempo original del sistema.
v= rapidez del reloj vista por el observador externo (igual que la rapidez externa de los dos observadores)
c= rapidez de la luz (300 000 m/s)
Antes de continuar, es importante reconocer que a esta cantidad:

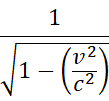
Se le conoce como factor de Lorentz, y es una constante que se puede representar con la letra griega gamma:

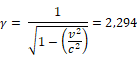
De modo que, sabiendo que gamma o factor de Lorentz es toda esa expresión, ahora podemos simplificar esa expresión de tiempo y usar esta:

La dilatación del tiempo ha sido uno de los aspectos cuya verificación permite el funcionamiento de los satélites GPS. Ya que los satélites están rotando a mucha altura, la gravedad terrestre es menor y eso afecta relativísticamente los relojes internos de ellos los cuales se adelantan respecto a la tierra unos 38 000 nanosegundos por día (aunque son relojes atómicos exactos, sincronizados con relojes similares en la tierra). De no hacerse esa corrección de tiempo, al ofrecer la posición de un objeto en la tierra lo haría con 11,7km de diferencia (incrementándose cada día). Imagine el Waze del auto de tu papá llevándolo a direcciones decenas o centenas de metros equivocado. (Más detalles aquí: http://www.relatividad.org/bhole/gps.htm#)

También los astronautas que viajan al espacio experimentan el retardo del tiempo, no por efectos de la velocidad sino principalmente por causa de la diferencia en el campo gravitacional. Un astronauta que pase 6 meses en la estación espacial MIR y regrese a la tierra encontrará a los terrícolas 6 meses y 44 milésimas de segundo más viejos. Un detalle importante de matizar es que para los terrícolas transcurrieron exactamente 6 meses, y para el astronauta también transcurrieron 6 meses. Cuando el astronauta cambia de sistema de referencia y se ubica en la tierra es cuando se percibe la diferencia temporal. (Más información aquí: http://www.elmundo.es/blogs/elmundo/apuntesnasa/2015/11/26/cuanto-viaja-en-el-tiempo-un-astronauta.html)

Una explicación y aplicación interesante es lo ocurrido con lo Muones. Los mounes aparecen en la alta atmósfera cuando los rayos cósmicos inciden con átomos pesados, descomponiéndolos y generando los famosos muones como uno de los subproductos. Pero la vida media de los muones es de 2,2 µs, y se esperaba que muy pocos llegaran a la superficie terrestre, pero en 1941 hiciron un experimento que mostró que a la tierra llegan más muones de lo esperado, eso únicamente podía significar una cosa: Los vida media de los mouones es más alta de lo esperado! Y eso se debe a que viajan a velocidades cercanas a la luz y por eso hay una dilatación del tiempo tal que les permite llegar hasta la tierra antes de desaparecer (más información http://naukas.com/2015/08/17/los-tramposos-muones-y-como-podemos-tocar-estrellas/).

Contracción de la longitud

Cuando los cuerpos se mueven a velocidades cercanas a la velocidad de la luz, también ocurre que los cuerpos van disminuyendo su longitud en la misma dirección del movimiento de acuerdo a la siguiente fórmula:

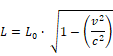Donde:

L= Longitud medida del objeto en movimiento.
L₀= Longitud medida del objeto cuando está en reposo.
v= rapidez relativa entre el objeto observado y el observador
c= rapidez de la luz (300 000 m/s).

Esta es una consecuencia de que la velocidad máxima de cualquier cosa sea la velocidad de la luz, porque al llegar a la velocidad de la luz la contracción será tan grande que no será posible identificarlo.

Esta es una ilustración de lo que ocurriría a una bola acelerada a la velocidad de la luz:

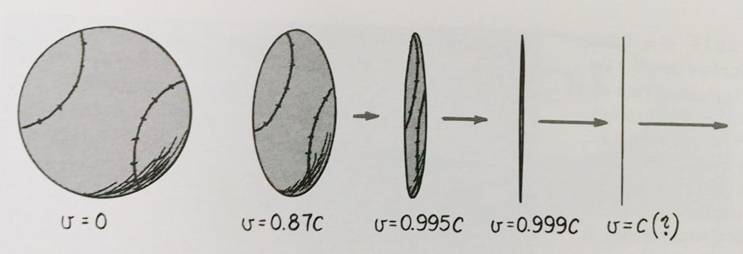
Un viejo verso en física, que explica poéticamente este hecho es:

Había una vez un joven esgrimista llamado Ben
De extraordinaria agilidad
Y tan rápido era su acción
Que la contracción de Lorentz
Redujo su espada hasta darle forma de disco.

Claro, llevar un macro cuerpo material a la velocidad de la luz es imposible, tanto por aspectos técnicos como mecánicos. Pero las partículas atómicas si experimentan estos fenómenos.

Ejercicios

Vida media de un muón en movimiento:
1) a) ¿Cuál será la vida media de un muón medida en el laboratorio si viaja a v=0,6c (1,8×10⁸ m/s) con respecto al laboratorio? Nota: su vida media en reposo es 2,2 x10^-6s.

b) A una velocidad de 1,6×10⁸ m/s la física clásica Newtoniana predice que la distancia que recorre este muón desde que se forma en la alta atmósfera será de:

Pero ellos logran llegar a la tierra, explique ¿por qué llegan a la tierra?, use al menos un cálculo.

2) Un automóvil viaja a 100 km/h recorre cierta distancia en 10 segundos según el reloj del conductor ¿qué intervalo de tiempo mide un observador en reposo en sobre la carretera? ¿Qué significa el resultado obtenido y por qué?

3) En una nave espacial en reposo en el espacio hay una ventana lateral de 1m de altura por 1,5m de largo. Entonces empieza a moverse y pasa de lado a la tierra, por la ventana el astronauta podría haber visto su antigua casa, entonces va a una velocidad de 0,9c,

• a) ¿Cuáles son las dimensiones de dicha ventana vistas por el mismo astronauta?

• b) ¿Cuáles son las dimensiones de dicha ventana vistas por un observador en la tierra?

4) Aplicación de Relatividad:

Un explorador del espacio de una era futura viaja a la estrella más cercana, Alfa-Centauro, en un cohete con velocidad v = 0,9c. La distancia de la Tierra a la estrella, medida desde la Tierra, es L = 4 años-luz (o 4c años). ¿Cuál esla distancia vista por el explorador, y cuánto pensaría él que dura el viaje a la estrella?

Respuestas:

1a) Solución:

Observe que “c” cancela a “c”, por eso no hace falta usar el valor de c=300 000 m/s.

1b) Llega a la tierra porque:

Logran recorrer 100 m adicionales gracias a la dilatación del tiempo.

2) v= 100 km/h = 27,8 m/s
t₀= 10s

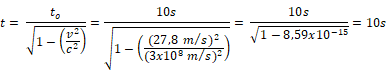
3)  a) Para el mismo astronauta dentro de la nave, la ventana no ha cambiado de tamaño, la sigue viendo de 1m x 1,5 m.

• b) solo se acorta en la dirección del movimiento, por lo tanto la altura con cambia solo la longitud en una magnitud de:

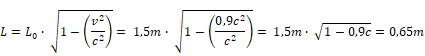
Entonces las dimensiones son: 1m alto x 0,65m largo.

4) La distancia L = 4c años es la distancia propia entre la Tierra y la estrella (que
asumimos que están en reposo relativo). Así que la distancia vista desde el cohete
viene dada por la fórmula de contracción de longitud como:
Lcohete = LT ierra                                                              (1)
γ

Si β = 0,9 entonces recordemos que la constante gamma vale γ = 2,3; así que:

         (2)

Podemos calcular el tiempo T del viaje de dos formas: visto desde el cohete, la
estrella está inicialmente a 17c años y está aproximándose con velocidad v = 0,9c.
Por tanto,

        (3)

(Nótese que los factores c se cancelan convenientemente cuando usamos c años
y medimos las velocidades como múltiplos de c).
Alternativamente, medido desde el sistema Tierra, el viaje dura un tiempo

             (4)

pero debido a la dilatación del tiempo este es “γ” veces Tcohete, que es, por tanto:

            (5)    de acuerdo con (3), por supuesto.

Nótese que la dilatación del tiempo (o la contracción de la longitud), permite un ahorro apreciable al piloto del cohete. Si vuelve puntualmente a la Tierra, entonces como resultado del viaje completo habrá envejecido sólo 38 años, mientras que su gemelo que se quedó habrá envejecido 8’8 años. Este resultado sorprendente, a veces conocido como la paradoja de los gemelos, es ampliamente verificado por los experimentos discutidos en la sección que trataba sobre la dilatación del tiempo. En principio, la dilatación del tiempo permitiría a los exploradores hacer en el tiempo de una vida viajes que requerirían cientos de años vistos desde la Tierra. Puesto que esto requiere cohetes que viajan muy cerca de la velocidad de la luz, ¡no es posible que pase pronto!

Práctica de Física Moderna:
Nota: recuerde que para acceder a la práctica como mínimo primero debe estar registrado como usuario.